Методы геометрических преобразований

Статьи о педагогике » Решение задач на построение в курсе геометрии основной школы как средство развития логического мышления школьников » Методы геометрических преобразований

Страница 2

Построение. Строим последовательно: прямую b', симметричную с прямой b относительно прямой а; точку С, общую для прямых с и b'; прямую ВС; точку О ВС а; точки А и D на прямой а, отстоящие от точки О на расстоянии ; ABCD — искомый ромб.

Доказательство ввиду его простоты опустим.

Исследование. Возможны следующие случаи: 1) с || b', решений нет; 2) с b', решений бесконечно много; 3) прямые с и b' пересекаются вне прямой а, одно решение; 4) прямые с и b' пересекаются на прямой а, решений нет.

Метод параллельного переноса

Параллельным переносом на вектор называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что вектор равен вектору .

Методом параллельного переноса решают задачи, при анализе которых трудно найти зависимость между данными элементами, позволяющую построить искомую фигуру (данные элементы удалены друг от друга); но если мы какую-нибудь часть или всю фигуру перенесем параллельно в некотором направлении на определенное расстояние, то получим вспомогательную фигуру, которую легко можно построить. Направление и величина переноса определяются так, чтобы во вспомогательную фигуру вошло большее число данных.

Рассмотрим задачу: “Построить выпуклый четырехугольник, зная три его угла и две противоположные стороны”.

Подробнее: даны два отрезка а и b и три угла α, β, δ. Требуется построить четырехугольник ABCD так, чтобы А = α, В = β, D = δ, AD = a, СВ = b. Предполагается, что 0° < α < 180°, 0° < β < 180°, 0°< δ < 180°.

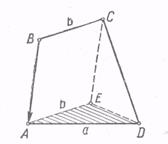
Рис. 5

Анализ. Допустим, что ABCD (рис. 5) — искомый четырехугольник. Перенесем сторону ВС на вектор , и пусть отрезок ВС займет после переноса положение АЕ. Тогда в AED известны: AD = a, AE = b, DAE = BAD –BAE = = A – (180° – B) = α + β – 180°. По этим данным AED может быть построен.

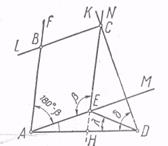
Рис. 6

Построение. 1) На произвольной прямой строим отрезок AD = а (рис. 6); 2) Через точку А проводим луч AM под углом α + β – 180° к лучу AD; 3) Откладываем на луче AM отрезок АЕ = b; 4) Строим луч EN, образующий с ЕА угол β и расположенный с точкой D по разные стороны от прямой AM; 5) Строим луч DK так, чтобы ADK был равен δ и чтобы луч DK располагался по ту же сторону прямой DE, что и луч EN; 6) Отмечаем точку С пересечения лучей EN и DK — третью вершину четырехугольника; 7) Четвертая вершина В получается в пересечении прямой AF, параллельной СЕ, с прямой CL, параллельной АЕ.

Доказательство. BAD = ВАЕ+DAE = (180° – β) + (α + β – 180°) = α. ABC = СЕА, как углы, стороны которых соответственно параллельны и противоположно направлены. СЕА = β по построению. ADC = δ по построению. Отрезок AD = а по построению. ВС = АЕ, как отрезки параллельных между параллельными. Но АЕ = b, а значит, и ВС = b.

Страницы: 1 2 3 4 5 6 7

Статьи по теме:

Попустительский стиль воспитания
«Попустительский стиль воспитания характеризуется своего рода «равнодушием» (чаще всего, неосознанным) со стороны педагога в отношении развития, динамики учебных достижений или уровня воспитанности с ...

Структура урока по лёгкой атлетике
Каждый урок физической культуры и здоровья, в том числе и легкой атлетики, состоит из трех функционально связанных составных частей: подготовительной, основной, заключительной. Последовательность эти ...

Значение подвижных игр в воспитании детей
Надежда Константиновна Крупская, говоря о значении игр в формировании личности ребенка, отмечала: «Игра есть потребность растущего детского организма. В игре развиваются физические силы ребенка, твер ...

Методы геометрических преобразований

Навигация